|
Einlitung: The world of
electronics is developing faster & faster. The demand for quality software
is ever increasing, meanwhile the complexity of hardware is also on the
rise. To understand how these diodes, transistors, thyristors, I.C.s &
eventually the hardware itself work, it is necessary to understand the basic
Physics behind these. That is noting but the "Theory Of Semiconductors ".
This article is a helping hand in
understanding the basic concepts, which are dealt with in detail. A suitable
analytical explanation is also provided for interesting readers who may be
studying this subject as part of their course. But for those, who just want
to have an overall idea, can simply skip the analytical description.
Prerequisites: Let
us list a few prerequisites,
i) An idea of atomic structure, Bohr's atomic model in particular.
ii) Crystal
structure basics.
iii) An idea of Heisenberg's Uncertainty Principle.
iv) Wave Mechanics & Schr´┐Żdinger Wave Equation.
v) De Brooglie's wave
Hypothesis of "Wave nature of matter".
Although all these are not necessary
but their knowledge is an advantage. A High School level of study of these
concepts is more than enough for our discussion.
Now Let us move on to the real thing,
Let Us brief Ourselves With a little bit
of preliminaries.
Atomic Structure: After a series of theories for the structure of an atom the most
successful were Rutherford's Model & Bohr's model.
We shall not see Rutherford's model, only a small account of Bohr's model
of Hydrogen and Hydrogen like particles.
Bohr's model of Hydrogen Atom
Bohr's atomic model is a refined version of Rutherford's model. it
assumes the following which
as we will see later, not to have any logical or theoretical
explanation then.
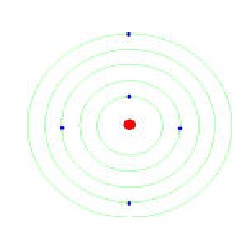
Postulates of Bohr's Theory:-
i) Electrons revolve round the positively charged nucleus in certain
definite circular orbits having certain definite energy.
ii) These are "stationary orbits " & Electrons can stay in these
orbits without radiating energy.
iii) Electrons absorb or emit energy whenever they jump from one
energy level to another in accordance with Planck's Quantization Rule.
i.e.
ΔE=hγ where, ΔE is the change in energy
h is the Planck's constant
γ is the
frequency of the of light emitted.
iv) Electrons revolve in only those circular orbits, in
which the angular momentum of the electron is Quantized (Quantization Rule).
i.e.
mvrn =nh/(2Π)
n= 1, 2, 3, . . . .
The graph energy vs. frequency is shown
here:
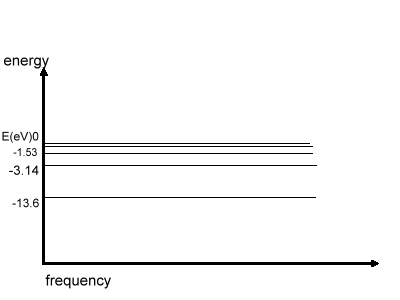
The above Fig. shows the energy distribution in
various levels in Hydrogen atom, E=0 when n= infinity, i.e. when e-
is out of the atom.
Note: We have not derived the values of energy, which
can be done assuming the Coulomb's Law & Bohr's Quantization Rule.
We may even derive the values of radius of Bohr's orbit & velocity of e-
in the orbit.*
Drawbacks of the Theory:- 1) It could not
explain the fine structure of spectrum.
2) No Explanation for the Quantization Rule.
3)Uncertainity
Principle Completely eliminates the possibility of having e-s
in specific circular orbits.
4)It cannot be applied to multi-electron systems.
Take Home:
An atom consists of a positively charged nucleus
around which e- revolve in definite quantized energy circular
orbits of only certain radii.
So, we shall be done with Bohr's model & move on to a
somewhat complicated Schr´┐Żdinger Wave Equation Solutions of Hydrogen atom &
further switch to, that our interest, Silicon atom.
*All the derivations are not done here, the reason being
the irrelevancy of the same in our study.
This Discussion of Bohr's Model can be extended to single e-
systems having any atomic number.
Before we move on Schr´┐Żdinger wave equation solutions
of Hydrogen atom, we shall learn something about Heisenberg's uncertainty
Principle.

Heisenberg's uncertainty
Principle
Heisenberg's uncertainty Principle state that,

i.e.
Δx.
Δpx ≥ h/(2Π)
Even the following are true according to Heisenberg's uncertainty
Principle,
ΔE . Δt
≥ h/(2Π),
Δθ . ΔL
≥ h/(2Π) where,
Δx is
the uncertainty in position
Δpx
is the uncertainty in momentum
E is the energy of the particle, t is the time spent the particle in the
energy state E,
θ is the angular
position, L is the angular momentum
Δ
represents the change or uncertainty
This means , we cannot measure the momentum & position of a particle
accurately, all we can say is the probability of finding the particle in a
region of space.
* The proof for
Heisenberg's uncertainty Principle
is out of the purview of our domain.
Although Heisenberg's uncertainty Principle
is inherently applicable to every system, it is not observable in macro
scale .

Schr´┐Żdinger
equation solutions of Hydrogen atom
Einlitung:
Luis De-Brooglie Hypothecated that if light can behave as waves &
particles, particles will also behave as waves under suitable conditions.
Due to the inherent wave nature of particles it is not possible to pin point
the location of a particle such as e-. We also know that, a wave
in space is always descripted by a differential equation known as 'Wave
equation' of the wave. Schr´┐Żdinger came out with an interesting mathematical
theory which gave the wave equation of matter. Though, the mathematical
function in Complex no.s did not have a direct physical interpretation but
later was found to give the probability of finding the particle if Squared &
taken modulus of as defined in complex domain.
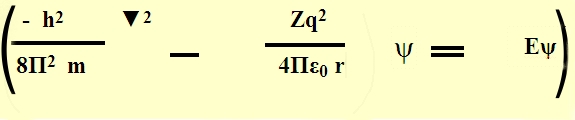
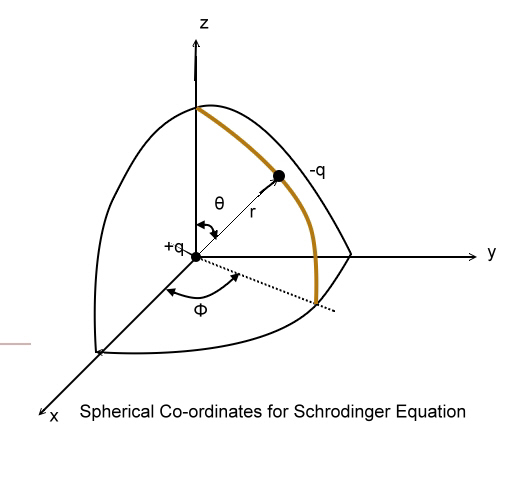
We shall not say any further about the form of
Schr´┐Żdinger wave equation the mathematical conditions posed on it & so on.
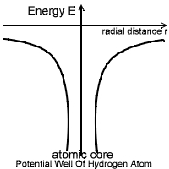
Potential Energy Distribution in hydrogen Atom:
The Hydrogen atom can be thought to have a nucleus of charge (+q) = 1 C.
fixed in position. The fig. shows the potential energy distribution of
Hydrogen atom, in which on e can observe that the potential energy (-ve) of
the atom is highest at infinity distance from the centre & zero at nucleus.
So, we have a complex Boundary conditions & a solution in 3-d.
We shall not solve the Schr´┐Żdinger wave equation But assume the same &
proceed.
The Schr´┐Żdinger wave equation is solved in polar coordinates by putting the
boundary conditions.
The solution is of the form,
ψ (r,θ,Φ)=R(r).P(Φ).Q(θ)
When we solve assuming the above as solution, to obtain a physically
feasible solutions , it requires us to have 3 Quantum no.s n, l, mc
called the Principal, azimuthal and Magnetic Quantum no.s.
Principal Quantum Number (n) :-
It is a measure of total energy of the e- .
It is also a measure of major axis of the elliptical orbit.
The energy levels are indicated as K, L, M, N, ... shells rather than
orbits. This is due to the inability to pin point the location of the e-
as per
Heisenberg's uncertainty Principle.
That means, there is no concept of radius of orbit as predicted by
Bohr, but all we can say is that, 'there is a high probability of locating
an e- at the distance given by the Principal Quantum Number'.
Further, we have Azimuthal Quantum Number (l), Magnetic Quantum Number
(ml) and Spin Quantum Number (ms) obtained while
solving the
Schr´┐Żdinger equation. Which give information about the Quantized Angular
Momentum, Direction of Angular Momentum and spin on the e-
respectively.
Observe The Table below and also the potential well of
Hydrogen atom
|
Shell |
n>0 |
0≤
l ≥n-1 |
-l
≤ ml ≤ l |
ms
= ´┐Ż 1/2 |
Levels |
Max Number of e- |
|
n |
l |
ml
|
ms |
| K |
1 |
0 |
0 |
´┐Ż 1/2 |
1s |
2 |
|
L |
2 |
0 |
0 |
´┐Ż 1/2 |
2s |
2 |
| 1 |
0 |
´┐Ż 1/2 |
2p |
6 |
| 1 |
-1 |
´┐Ż 1/2 |
| 1 |
+1 |
´┐Ż 1/2 |
|
M |
3 |
0≤ l ≥2
|
-2 ≤ ml
≤ 2
|
´┐Ż 1/2 |
3s |
2 |
|
´┐Ż 1/2 |
3p |
6 |
|
´┐Ż 1/2 |
3d |
10 |
Table
of Quantum Number
So, Now in the next article we will see what impact
does this concept make on multi electron systems and Silicon in particular.

About next Article: This was just preliminaries to semiconductor
theory. In the coming articles, that will be available online soon, we will
learn the atomic structure of the Silicon atom, Silicon Crystal, intrinsic
and extrinsic Semiconductors and further.
 |